Line Drawing Algorithms - Bresenham / Mid Point Algorithms
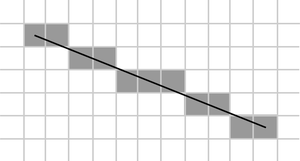 The line is drawn between two points (x0, y0) and (x1, y1), where these pairs indicate column and row, respectively, increasing in the down and right directions. We will initially assume that our line goes down and to the right, and that the horizontal distance x1-x0 exceeds the vertical distance y1-y0 (that is, the line has a slope less than 1.) Our goal is, for each column x between x0 and x1, to identify the row y in that column which is closest to the line and plot a pixel at (x,y).
Now, how do we figure out which pixel is closest to the line for a given column? The general formula for the line between the two points is given by:
The line is drawn between two points (x0, y0) and (x1, y1), where these pairs indicate column and row, respectively, increasing in the down and right directions. We will initially assume that our line goes down and to the right, and that the horizontal distance x1-x0 exceeds the vertical distance y1-y0 (that is, the line has a slope less than 1.) Our goal is, for each column x between x0 and x1, to identify the row y in that column which is closest to the line and plot a pixel at (x,y).
Now, how do we figure out which pixel is closest to the line for a given column? The general formula for the line between the two points is given by:
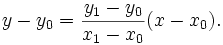 Since we know the column, x, the pixel's row, y, is given by rounding this quantity to the nearest integer:
Since we know the column, x, the pixel's row, y, is given by rounding this quantity to the nearest integer:
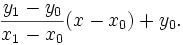 However, explicitly calculating this value for each column, x, is silly; we need only note that y starts at y0, and each time we add 1 to x, we add the fixed value (y1-y0)/(x1-x0), which we can precalculate, to the exact y. Moreover, since this is the slope of the line, by assumption it is between 0 and 1; in other words, after rounding, in each column we either use the same y as in the previous column, or we add one to it.
However, explicitly calculating this value for each column, x, is silly; we need only note that y starts at y0, and each time we add 1 to x, we add the fixed value (y1-y0)/(x1-x0), which we can precalculate, to the exact y. Moreover, since this is the slope of the line, by assumption it is between 0 and 1; in other words, after rounding, in each column we either use the same y as in the previous column, or we add one to it.
//Program to plot line by Bresanham's Approach
#include <iostream.h>
#include <graphics.h>
#include <math.h>
#include <conio.h>
void drawline(int x1, int y1, int x2, int y2)
{
int temp,p, dx, dy;
dx=abs(x2-x1);
dy=abs(y2-y1);
float m;
m=float(y2-y1)/float(x2-x1)>0?2:1;
if (abs(x2-x1)>abs(y2-y1))
{
if (x2<x1)
{
temp=x2;
x2=x1;
x1=temp;
temp=y2;
y2=y1;
y1=temp;
}
int x=x1,y=y1;
p=2*dy-dx;
while (x<x2)
{
x++;
if (p<=0)
p+=2*dy;
else
{
p+=2*(dy-dx);
y=y+pow(-1,m);
}
putpixel(x+getmaxx()/2,getmaxy()/2-y,5);
}
}
else
{
if (y2<y1)
{
temp=x2;
x2=x1;
x1=temp;
temp=y2;
y2=y1;
y1=temp;
}
int x=x1,y=y1;
p=2*dx-dy;
while (y<y2)
{
y++;
if (p<=0)
p+=2*dx;
else
{
p+=2*(dx-dy);
x=x+pow(-1,m);
}
putpixel(x+getmaxx()/2,getmaxy()/2-y,5);
}
}
}
void main()
{
int x1, x2, y1, y2;
int gdriver = DETECT, gmode, errorcode;
initgraph(&gdriver, &gmode, "");
line(0,getmaxy()/2,getmaxx(),getmaxy()/2);
line(getmaxx()/2,0,getmaxx()/2,getmaxy());
cout<<"Enter x1 ";
cin>>x1;
cout<<"Enter y1 ";
cin>>y1;
cout<<"Enter x2 ";
cin>>x2;
cout<<"Enter y2 ";
cin>>y2;
drawline(x1,y1,x2,y2);
getch();
}